

0 引言
由于數字調制信號越來越多地應用于通信信號處理領域,因此對數字信號調制識別的研究也越來越多。傳統的調制識別的判決方法有:決策判決法、高階累積量算法和人工神經網絡算法等。但是決策判決法在低信噪比環境中識別率不高,而基于人工神經網絡的識別方法計算復雜度較高。信號的高階累積量算法具有很好的抗噪性能,故對基于高階累積量的通信信號調制識別算法的研究受到了廣泛重視。文獻利用高階累積量實現了對 2ASK/BPSK,4ASK,4PSK,2FSK,4FSK信號的分類。文獻利用四階和六階累積量實現了對 2ASK,4ASK,8ASK,QPSK,8P-SK,16QAM信號的分類。文獻利用二、四、六階累積量實現了對 2ASK/BPSK,4ASK,QPSK,2FSK,4FSK,8FSK,16QAM信號的分類。文獻對高階累積量的四階、五階累積量進行了優化和仿真,但是在低信噪比的環境下,對信號的識別率都不高。
在尋找更優識別算法的過程中,以往的研究更多的把注意力放在了識別算法上,而沒注重算法的硬件設計與實現。System Generator for DSP是Xilinx公司開發的一款理想的DSP開發軟件,它對數字信號處理單元進行系統建模,并將模型轉換成可靠的硬件實現,是連接數字信號處理高層系統設計與Xilinx FPGA實現的橋梁。針對上述問題,本文提出了高階累積量的改進算法,并在System Generator中實現了算法的FPGA設計。
1 高階累積量的改進算法
數字信號的調制識別通常經過三個步驟:接收信號預處理、特征參數提取和調制方式識別。然而實現信號調制識別的關鍵環節是從接收信號中提取出用于識別的特征參數。下面首先介紹高階累積量算法是如何提取用于調制識別的特征參數的。
1.1 特征參數的提取
首先給出高階矩的定義,對于一個具有零均值的復隨機過程X(t),其p階混合矩可表示為:Mpq=E[X(t)p-qX*(t)q]。其中,*表示函數的共軛。然后定義高階累積量如下:

設信號的能量為E,利用文獻中提出的算術平均來代替統計平均的方法,計算各種數字調制信號的高階累積量,得到高階累積量的理論值,如表1所示。
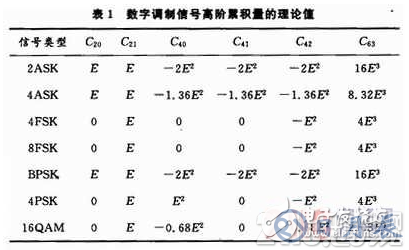
從表1中可以看出,從信號的高階累積量中提取特征參數,可以實現大部分信號的分類,而由于2ASK和BPSK信號的各累積量值相同,故利用高階累積量無法實現其分類。MFSK的高階累積量也相同,直接利用累積量無法實現其類內識別。
由文獻知,對MFSK信號求導,再經中值濾波,在濾除含有沖激函數的項后,再計算所得信號的高階累積量值,如表2所示。
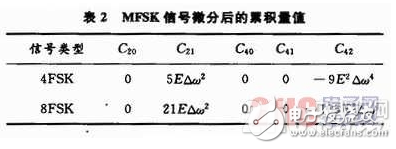
由以上分析可知,為了實現數字調制信號的調制識別,利用不同的累積量組合,從中提取了以下4個特征參數,定義如下:
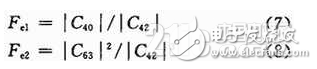
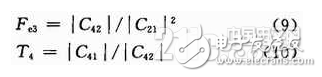
1.2 信號的調制識別流程
在低信噪比環境中,基于高階累積量的數字調制信號識別算法對2ASK和4ASK信號的識別率普遍較低。針對此問題,本文提出了高階累積量的改進算法。文中在高階累積量算法的基礎上,對四個特征參數的判決順序稍作調整,將MASK信號與其他信號分離,取得了較好的效果。具體識別過程如下:
(1)用編程工具編程產生各種數字調制信號,并加入信噪比已知的噪聲,作為待識別的信號。
(2)將接收到的待識別信號通過下變頻直接變換到零頻,然后利用正交下變頻技術得到復基帶調制信號。
(3)計算各種待識別信號的二、四、六階累積量,并計算其特征參數Fe1,Fe2,T4。
(4)利用特征參數T4的識別,可以將信號分為兩組:第一組為MASK信號,第二組為MPSK,16QAM,MFSK信號。利用Fe2的閾值(t1)實現
第一組組內識別;再利用Fe2的另一個閾值(t2)和Fe1從第二組中識別出16QAM,MPSK信號。
(5)將待識別信號進行微分后再經中值濾波器,計算變換信號的高階累積量,并計算特征參數Fe3,利用Fe2實現MFSK類內識別。
在信號的調制識別過程中,主要是根據決策樹方法進行分類和識別。本文在提取上述四個特征參數的基礎上,根據不同的決策規則建立決策樹。經過多次性能的仿真和比較,最終得到一種比較好的識別算法,如圖1所示。其中t0,t1,t2,t3,t4都是閾值。
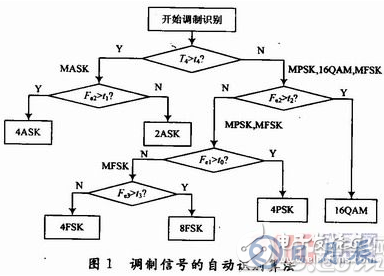
1.3 仿真結果
文中采用高階累積量的改進方法,對算法識別性能做蒙特卡洛仿真。給閾值t0,t1,t2,t3,t4設置合適的值后,再將1 000次獨立實驗得到的仿真結果取平均。在每次試驗中,設置信號的載波頻率為12 kHz,碼元速率為1 200 b/s,其中4FSK,8FSK的頻偏分別為1.5 kHz,3.5 kHz,碼元個數為200。圖2為原算法仿真結果,圖3為本文算法的仿真結果。

對圖2和圖3進行比較,可以看出本文算法的識別效果有了顯著提高。在信噪比為2 dB時,本文算法對16QAM信號和4PSK信號識別率達到100%,而原算法幾乎不能識別16QAM信號;在信噪比為4 dB時,對2ASK,4ASK信號的識別率分別為93%,100%。在信噪比為8 dB時,所有信號的識別率都可以達到90%以上,原算法有的信號識別率低于90%。比較后可知,在低信噪比環境下本文的算法對2ASK,4ASK,4PSK,16QAM信號的識別率有了顯著提高。
2 算法的System Generator設計
目前,FPGA芯片已成為數字信號處理系統的核心器件。由于DSP設計者通常對C語言或Matlab工具很熟悉,卻不了解硬件描述語言VHDL,使得FPGA并未在數字信號處理領域獲得廣泛應用。System Generator在很多方面擴展了MathWorks公司的Simulink平臺,提供了適合硬件設計的數字信號處理建模環境,加速、簡化了FPGA的DSP系統級硬件設計。通過Simulink的設計,System Generator即可自動完成硬件比特流的產生,從而高效的實現FPGA設計。
在FPGA調試和開發過程中,采用Xilinx公司的系統級建模工具System Generator構建信號調制識別的算法模塊,開發板選用Virtex-4。算法模塊主要由信號產生模塊,信號參數提取模塊和信號判決模塊構成。
2.1 調制信號的產生
在System Generator設計過程中,各種調制信號是利用Matlab語言編程提供的,并疊加上已知信噪比的高斯白噪聲。文中測試了2ASK,4ASK,4PSK,16QAM,4FSK和8FSK信號的識別率。
2.2 微分前參數提取模塊
提取特征參數Fe1,Fe2,T4的模塊,如圖4所示。其中,signal是信號源,DDS,FIR,DowSamp共同實現復基帶信號的同向分量和正交分量的提取,calculatmodule是計算Fe1,Fe2,T4三個特征參數的模塊,且這三個特征參數的結果分別由三個示波器輸出。
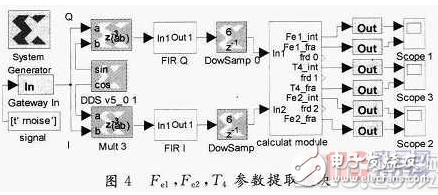
2.3 微分后參數提取模塊
提取特征參數Fe3的模塊,如圖5所示。其中,dmfilt是微分中值濾波模塊,兩個Black Box是計算特征參數Fe3的模塊。待識別調制信號經過dmfilt模塊后,然后由DDS,FIR,DowSamp等提取同向分量和正交分量,再通過計算Fe3的模塊計算參數,最后結果由Scope輸出。
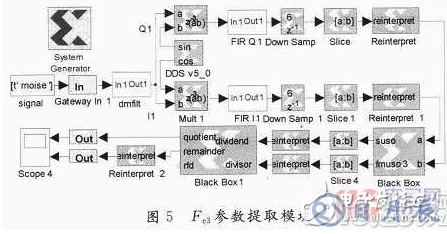
圖6是當信號為4FSK時,計算得到的Fe3值。其中,O.03~O.1 s是模塊計算參數的過程,O.1 s時對應的數據是計算的最終結果。將結果輸出到Matlab變量空間workspace中,可以得到在0.1 s時計算的Fe3值為12.4。
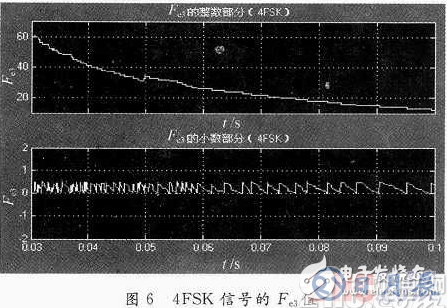
3 實驗結果
為了驗證調制識別系統的可行性,分別在Simulink和目標開發板上運行該設計。在產生硬件協同仿真模塊之前,先調用Resource Esti-mator模塊對本系統所需資源進行估測。估測結果見表3。
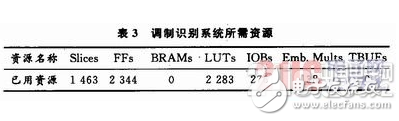
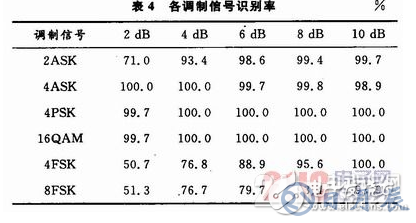
由于所需芯片內部資源較多,所以選用Virtex4-xc4vlx200芯片。然后在System Generator模塊中點擊Generate產生硬件協仿真模塊,并將它拖入到設計文件當中。給Virtex-4目標板上電,連接好JTAG口,啟動硬件協同仿真。當信號分別為2ASK,4ASK,4PSK等調制信號時,測試整個設計系統判決的結果,并將1 000次獨立試驗得到的仿真結果取平均,得到各種調制信號的識別率,如表4所示。從試驗結果來看,調制識別系統設計的FPGA硬件協同實現與Simulink仿真的結果基本一致,達到了設計的要求,從而也說明了System Generator有很高的精度。
4 結語
本文采用高階累積量改進算法對各種數字信號進行調制識別,大大提高了低信噪比環境下2ASK,4ASK,4PSK和16QAM信號的識別率,并在 System Generator中實現了高階累積量改進算法的FPGA設計,從模型的建立到FPGA的實現都是在圖形化設計環境下完成的,避開了編寫復雜VHDL語言的環節,且轉化到FPGA上實現的性能好,設計過程簡便靈活,從而為調制方式識別算法的設計提供了一種新的方案。利用System Generator提供的圖形化建模環境和自動轉換成VHDL代碼的能力,設計者可以將更多的時間和精力放在算法的優化上,同時又能顯著縮短設計開發周期。