131 1300 0010
設(shè)計背景：
二進(jìn)制轉(zhuǎn)十進(jìn)制在設(shè)計應(yīng)用中十分的廣泛。尤其在AD轉(zhuǎn)化中是必須所用到的一個小知識點(diǎn)，學(xué)習(xí)二進(jìn)制轉(zhuǎn)十進(jìn)制的方法顯的非常的重要。今天就和筆者來學(xué)習(xí)二進(jìn)制轉(zhuǎn)十進(jìn)制的方法，通過簡單的學(xué)習(xí)來掌握這么一門知識。
設(shè)計原理:
本次的設(shè)計主要是一個簡單的二選一數(shù)據(jù)選擇器，我們的設(shè)計主
二進(jìn)制中只有 0 和 1 兩個狀態(tài)，可以表示 0、1 兩種狀態(tài)的電 子器件很多，如開關(guān)的接通和斷開，晶體管的導(dǎo)通和截止、磁元 件的正負(fù)剩磁、電位電平的低與高等都可表示 0、1 兩個數(shù)碼。使 用二進(jìn)制，電子器件具有實(shí)現(xiàn)的可行性。
二進(jìn)制數(shù)的運(yùn)算法則少，運(yùn)算簡單，使計算機(jī)運(yùn)算器的硬件結(jié) 構(gòu)大大簡化。由于二進(jìn)制 0 和 1 正好和邏輯代數(shù)的假（false）和 真（true）相對應(yīng)，有邏輯代數(shù)的理論基礎(chǔ)，用二進(jìn)制表示二值 邏輯很自然。電子器件中，所有的數(shù)據(jù)都是用二進(jìn)制來表示的。
2. BCD 碼
BCD 碼（Binary-Coded Decimal）亦稱二進(jìn)碼十進(jìn)數(shù)或二-十進(jìn)制代碼。用 4 位二進(jìn)制數(shù)來表示 1 位十進(jìn)制數(shù)中的 0~9 這 10 個 數(shù)碼。BCD 碼是一種二進(jìn)制的數(shù)字編碼形式，用二進(jìn)制編碼的十 進(jìn)制代碼。BCD 碼這種編碼形式利用了四個位元來儲存一個十進(jìn) 制的數(shù)碼，使二進(jìn)制和十進(jìn)制之間的轉(zhuǎn)換得以快捷的進(jìn)行。
3. 實(shí)現(xiàn)方法
1) 對 10 求余法
將需要轉(zhuǎn)換的數(shù)字除以“權(quán)”，然后對 10 求余，得出數(shù)字各個 位上的數(shù)字。例如：8’b1000_0000（10 進(jìn)制中的 128），將此數(shù) 字對 10 求余，得出個位“8”，然后將“8”賦給最低的 4 位。將 此數(shù)字（128）除以 10，得出 12（在 FPGA 計算中，自動取整）， 對 10 求余，然后得出十位“2”，把“2”賦給次低的 4 位。將此 數(shù)字（128）除以 100，得出 1，對 10 求余，然后得出百位“1”， 把“1”賦給另外的 4 位。這樣就轉(zhuǎn)換出了 BCD 碼。
這類方法中，利用了大量的除法和求余，占用了大量的邏輯資 源。但是，實(shí)現(xiàn)比較簡單，如果芯片的邏輯資源足夠的話，可以 采取使用這種方法。
2) 大四加三法
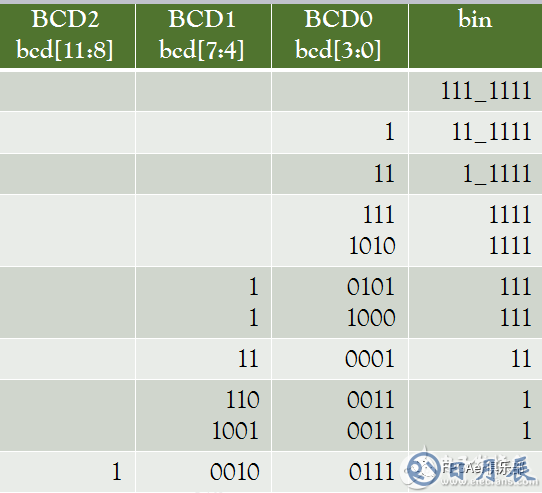
進(jìn)行移位，然后進(jìn)行判斷。如果大于四，則加三。最后得出我們想要的 BCD 碼（下述是按照轉(zhuǎn)換 7 位講解的原理）。
架構(gòu)圖如下
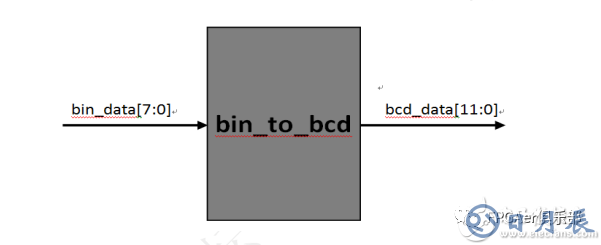
bin_data[7:0]:輸入的二進(jìn)制數(shù)據(jù)。
bin_data[11:0]:輸出的BCD碼（輸入的二進(jìn)制數(shù)據(jù)為8位，最大 為8’b1111_1111(255),每四位二進(jìn)制表示一個BCD碼，故而12位）。
設(shè)計代碼:
設(shè)計模塊
module bin_to_bcd(bin, bcd);
input [7:0] bin;
output [11:0] bcd;
wire [19:0] shift_reg [5:0];
assign shift_reg[5] = {9'b0,bin,3'b0};
bcd_modify u1(.bcd_in(shift_reg[5]), .bcd_out(shift_reg[4]));
bcd_modify u2(.bcd_in(shift_reg[4]), .bcd_out(shift_reg[3]));
bcd_modify u3(.bcd_in(shift_reg[3]), .bcd_out(shift_reg[2]));
bcd_modify u4(.bcd_in(shift_reg[2]), .bcd_out(shift_reg[1]));
bcd_modify u5(.bcd_in(shift_reg[1]), .bcd_out(shift_reg[0]));
assign bcd = shift_reg[0][19:8];
endmodule
module bcd_modify(bcd_in, bcd_out);
input [19:0] bcd_in;
output [19:0] bcd_out;
wire [19:0] bcd_reg;
bcd_sigle_modify u1(.bcd_in(bcd_in[19:16]), .bcd_out(bcd_reg[19:16]));
bcd_sigle_modify u2(.bcd_in(bcd_in[15:12]), .bcd_out(bcd_reg[15:12]));
bcd_sigle_modify u3(.bcd_in(bcd_in[11:8]), .bcd_out(bcd_reg[11:8]));
assign bcd_reg[7:0] = bcd_in[7:0];
assign bcd_out = {bcd_reg[18:0],1'b0};
endmodule
module bcd_sigle_modify(bcd_in, bcd_out);
input [3:0] bcd_in;
output reg [3:0] bcd_out;
always @ (*)
begin
if (bcd_in > 4)
bcd_out = bcd_in + 3;
else
bcd_out = bcd_in;
end
endmodule
測試模塊
`timescale 1ns/1ps
module tb();
reg [7:0] bin;
wire [11:0] bcd;
initial begin
bin = 255;
#500 bin = 20;
#500 bin = 125;
#500 $stop;
end
bin_to_bcd bin_to_bcd_dut(
.bin(bin),
.bcd(bcd)
);
endmodule
仿真圖:
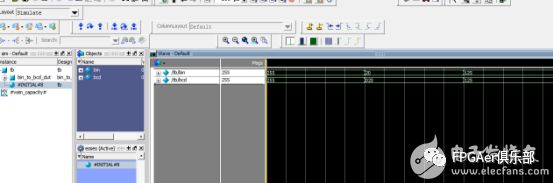
從仿真中可以看出本次設(shè)計的正確性，測試中我們輸出的二進(jìn)制和為8個1也就是255，轉(zhuǎn)化為10進(jìn)制后 按16進(jìn)制顯示，也就是255，通過驗證設(shè)計正確。
